尺度函數(shù)族
眾所周知,小波變換的雙正交基就來自與小波函數(shù)和尺度函數(shù),而他們通過scale和平移來得到的小波函數(shù)族和尺度函數(shù)族表示了不同小波(尺度)函數(shù)的分辨率,下面來用公式回顧一下:
小波函數(shù)定義

尺度函數(shù)分辨率沿拓
事實上,尺度函數(shù)族中的尺度 j 決定著不同的時間分辨率
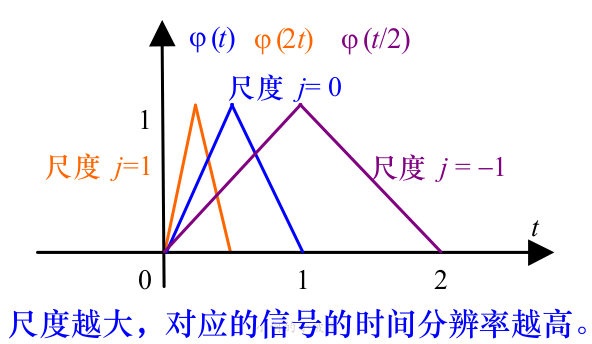
而實際上(證明請看參考資料),高時間分辨率的尺度函數(shù)必然可以代表低時間分辨率的尺度函數(shù),如上圖的三角尺度函數(shù)可以表示為:
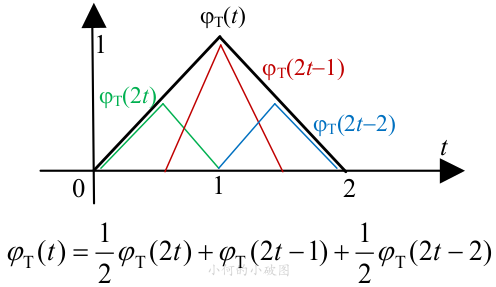
多分辨分析(MRA)方程
尺度函數(shù)的MRA方程
有了上面的鋪墊,這里就比較簡單了,因為我們知道,低分辨率信號可以由高分辨率信號線性表達,所以我們可以看出,高分辨率信號所張成的空間必然包含低分辨率張成的空間:


小波函數(shù)的MRA方程
講小波函數(shù)的MRA方程之前,我們不妨來回顧一下IDWT的定義:

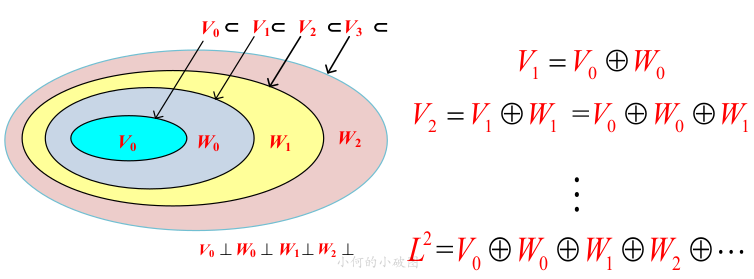
自然而然,我們可以知道小波函數(shù)的MRA方程的遞歸意義是更為重要的,所以有:
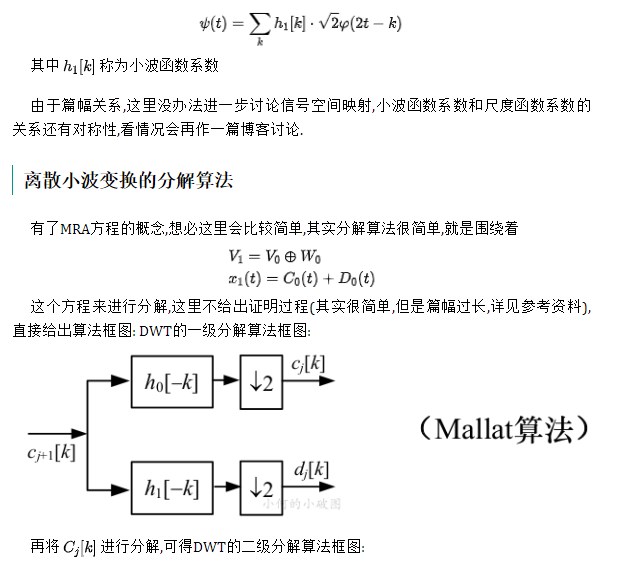

所以多級的大家也會求了吧...
可以簡單地看出,信號經(jīng)過小波函數(shù)系數(shù)(尺度函數(shù)系數(shù))之后還需要經(jīng)過一個抽取的過程,這個的話自己看看小波函數(shù)和尺度函數(shù)的定義式就可以了
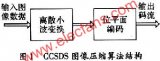
離散小波變換的重構(gòu)算法
這里是相似的,而且由于懶的原因我沒有做重構(gòu),所以也直接放圖:
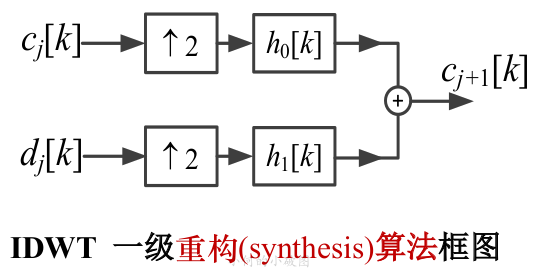

可以簡單地看出,信號經(jīng)過小波函數(shù)系數(shù)(尺度函數(shù)系數(shù))之后還需要經(jīng)過一個內(nèi)插的過程,這個的話自己看看小波函數(shù)和尺度函數(shù)的定義式就可以了.
需要注意的是,可以先抽取再濾波,但是不能先濾波后內(nèi)插,見上圖,(常識)
小波變換(DWT)的FPGA實現(xiàn)
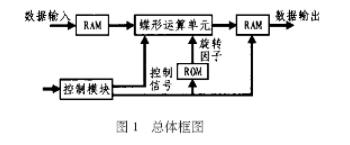
眾所周知,這次我們要實現(xiàn)的算法框圖是這個:
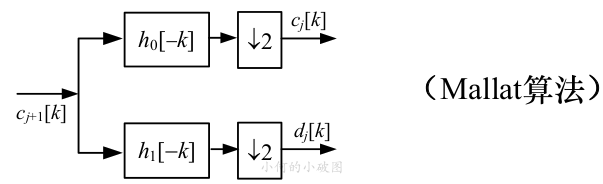
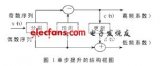
多相結(jié)構(gòu)模型
本來我是直接按照算法流程實現(xiàn)了DWT,然后講抽取和濾波對調(diào)了位置(為了提高系統(tǒng)的性能)
后來從網(wǎng)上僅有的資料中查看到別人做了多相分解,后面我想了想,如果不用多相結(jié)構(gòu)的話,相當(dāng)于原信號的先經(jīng)過了一次抽取,也是極大地浪費了信號. 又有:
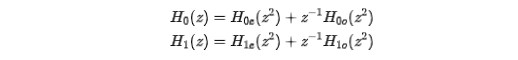
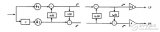
所以我們將信號和濾波器系數(shù)都進行奇偶分解,分別進行濾波,得到整體FPGA框圖:

接下來我們簡單地理一下過程
- 以db4小波為示例,其他小波只需要改改濾波器和matalb就可以了
- 僅實現(xiàn)一級分解,多級分解只要自己認真看博客就知道怎么做了
信號奇偶分解:
這個模塊比較簡單,但是想設(shè)計好需要一點小心思,思路就是做一個二分頻時鐘,上升沿將數(shù)據(jù)寫入偶數(shù)部分,下降沿將數(shù)據(jù)寫入奇數(shù)部分,這里不給出代碼
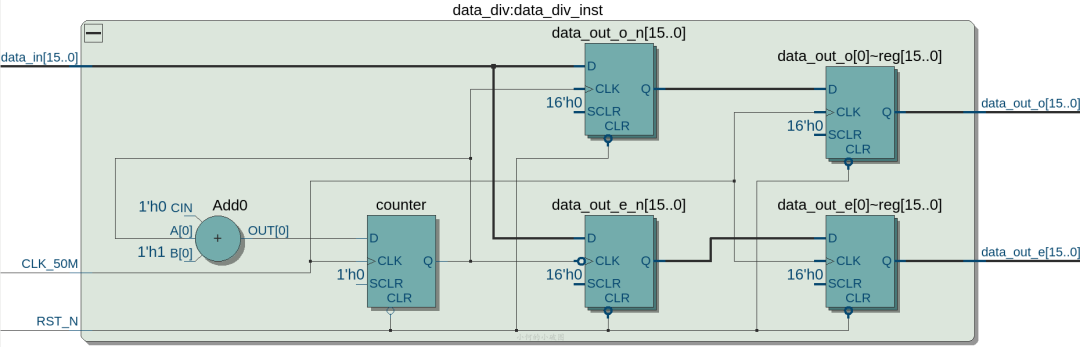
matlab獲取濾波器系數(shù)
代碼很簡單,先生成,再量化:
wn='db4';
[Ld,Hd,Lr,Hr] = wfilters(wn);
k=0:length(Ld)-1;
subplot(221);stem(k,Ld);
title('低通分解濾波器Ld');
subplot(222);stem(k,Lr);
title('低通重建濾波器Lr');
subplot(223);stem(k,Hd);
title('高通分解濾波器Hd');
subplot(224);stem(k,Hd);
title('高通重建濾波器Hr');
qua_ld = round(Ld*2^8);
qua_hd = round(Hd*2^8);
qua_lr = round(Lr*2^8);
qua_hr = round(Hr*2^8);
disp(qua_ld);
disp(qua_hd);
disp(qua_lr);
disp(qua_hr);
FPGA設(shè)計濾波器
這里的流程跟我上一篇博客,FPGA/Verilog 設(shè)計FIR濾波器 ^[2]^ 是相似的,這里不多說,給出一個濾波器的源碼:
module filter_hd_e(
//clock and reset
input CLK_50M,RST_N,
//filter in out
input signed [15:0] data_in_hd_e,
output signed [19:0] hd_out_e
);
localparam COEFF1,COEFF3,COEFF5,COEFF7; //過長省略
wire signed [19:0] add_result;
reg signed [15:0] data_shift[3:0];
wire signed [23:0] mul_data[3:0];
add_final add_inst(
.clock (CLK_50M),
.data0x (mul_data[0][23:8]),
.data1x (mul_data[1][23:8]),
.data2x (mul_data[2][23:8]),
.data3x (mul_data[3][23:8]),
.result (add_result)
);
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)begin
data_shift[0] <= 0;
data_shift[1] <= 0;
data_shift[2] <= 0;
data_shift[3] <= 0;
end
else begin
data_shift[3] <= data_shift[2];
data_shift[2] <= data_shift[1];
data_shift[1] <= data_shift[0];
data_shift[0] <= data_in_hd_e;
end
end
mult mult_inst_1 ( data_shift[0] *COEFF1 //下同
mult mult_inst_2 (
mult mult_inst_3 (
mult mult_inst_4 ( //過長省略
assign hd_out_e = add_result;
endmodule
大家對應(yīng)這框圖可能會說我怎么沒有把濾波器系數(shù)給翻轉(zhuǎn),這個問題的話,大家可以看看那個獲取系數(shù)的函數(shù)描述,他本來就幫我們翻轉(zhuǎn)了.
加法器就算了,過于簡單
matlab產(chǎn)生激勵
這個在上一篇博客中也有提及,但是這次我們不是直接產(chǎn)生mif文件,而是選擇在仿真的時候讀入數(shù)據(jù),所以代碼就是:
depth = 1024;
width = 16;
x = 0 : 2*pi/(depth-1) :2*pi;
y = sin(x)+sin(8*x);
y = (y/2) * 32768;%將信號放大32768倍
y(360:400) = 32767; //為了小波變換的戲劇性效果設(shè)置
b = signed2unsigned(y,width);
fid = fopen('sinx.txt','wt'); %將信號寫入一個.txt文件中
for num=0 : (depth-1)
fprintf(fid,'%x\\n',round(b(num+1)));
end
fclose(fid);
仿真結(jié)果
用tb讀入數(shù)據(jù):
integer i; //數(shù)組坐標(biāo)
reg signed [15:0] stimulus[1:data_num]; //數(shù)組形式存儲讀出的數(shù)據(jù)
initial
begin
RST_N = 1'b1;
#60 RST_N = 1'b0;
#60 RST_N = 1'b1;
$readmemh("sinx.txt", stimulus); //將txt文件中的數(shù)據(jù)存儲在數(shù)組中
i = 0;
repeat(data_num) begin //重復(fù)讀取數(shù)組中的數(shù)據(jù)
i = i + 1;
data_in = stimulus[i];
#PERIOD; //每個時鐘讀取一次
end
$stop;
end
那么又到了緊張刺激的,看波形環(huán)節(jié): matlab計算:
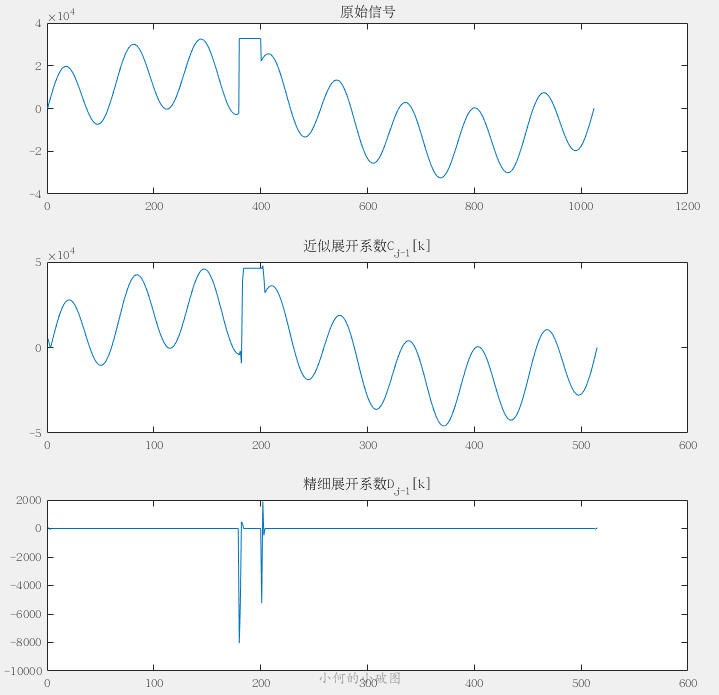
fpga計算:

 電子發(fā)燒友App
電子發(fā)燒友App


























評論